Distribusi Probabilitas (1 Dimensi)

Dalam pembahasan kali ini, kita hanya akan meninjau partikel yang bergerak dalam arah sumbu-x saja. Namun, bukan berarti hanya sumbu-x saja yang boleh kita gunakan, anda juga boleh memilih sumbu-y atau sumbu-z (sesui dengan selera) dengan syarat anda harus konsisten dengan pilihan anda.

Untuk sebuah partikel yang bergerak dalam arah x,

Jumlah keadaan kuantum dalal interval momentum sebanding dengan panjang interval tersebut ().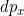
dan 

Probabilitas sebuah partikel berada pada salah satu keadaan kuantum tersebut sebanding dengan 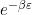(distribusi kanonik)

Dengan demikian probabilitas sebuah partikel memiliki momentum dalam interval adalah:

Kita ketahui bahwa:

Sehingga persamaan probabilitasnya menjadi:

( persamaan 1)

C merupakan konstanta.

Untuk mencari nilai C ini kita ingat bahwa jumlah nilai probabilitas adalah 1.

Subtitusikan persamaan (1) ke persamaan di atas:

(persamaan 2)

Misalkan

(persamaan 3)
kemudian didiferensialkan menjadi:


lalu kita subtitusikan nilai px pada persamaan 3 ke persamaan di atas, diperoleh:
(persamaan 4)
subtitusikan kembali persamaan 3 dan persamaan 4 ke persamaan 2! Diperoleh:





karena , maka:



hasil dari , maka:





Akhirnya diperoleh nilai C:
(persamaan 5)
Dengan mensubtitusikan persamaan 5 ke persamaan 1, diperoleh distribusi probabiltas untuk 1 dimensi sebagai berikut:



Materi ini diperoleh dari perkuliah fisika statitik di Jurusan Pendidikan Fisika UPI.
Kalo ada yang mau bertanya silahkan tanyakan di kolom komentar saja ya! (mudah-mudahan saya bisa menjawabnya... he he.., maklum masih belajar)